Let’s say embedded something on useful dimensions. Vector similarity checks if two items are similar on all dimensions. But when I want to build a graph from them, it may be better to require that they only share some properties. Humans need for example only a big enough overlap of shared interests to connect to each other. None is bad, being the exact same person is boring, too.

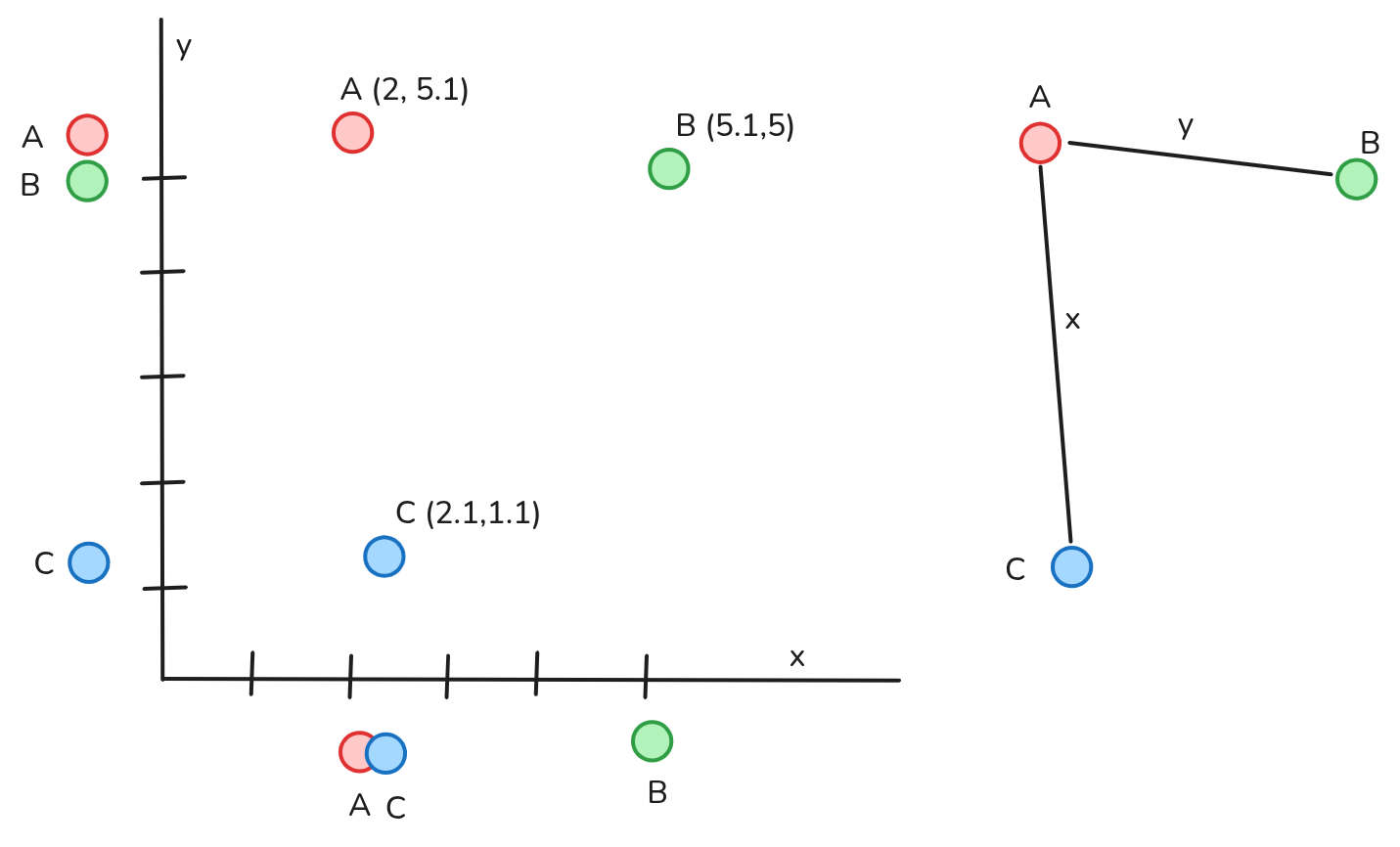We project the embeddings of the items down on a subset of axis and look, which ones are close there. This gives us a graph between the items.

But how to express this non-visually? Common distances weight all dimensions the same. But we want to weight it much much more if two items are similar on single or a subset of dimensions. We combine two vectors elementwise on each dimension. If they are very similar, we want a very big value, if they are not similar a very small value. This should change non-linearly.

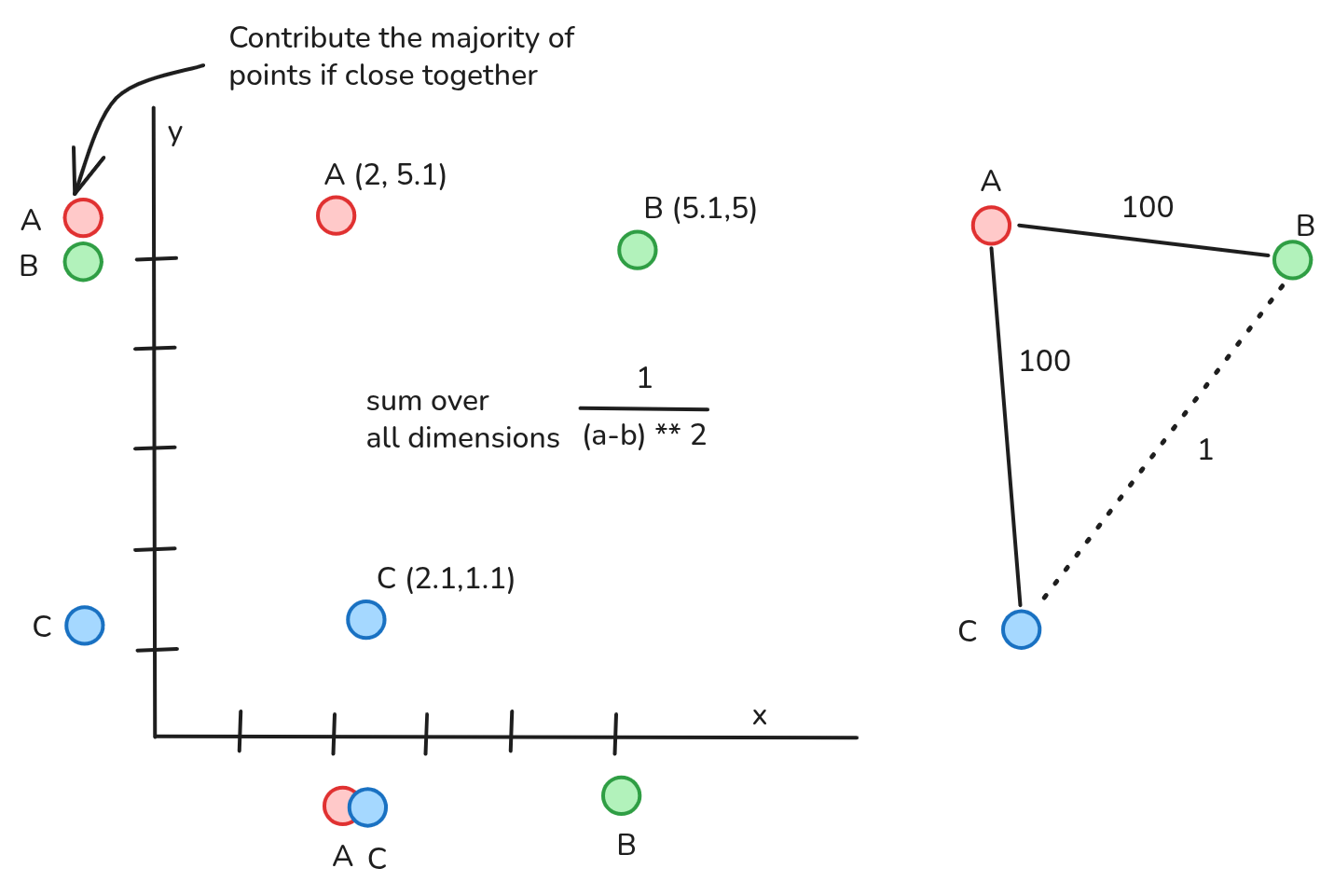
Squaring the differences comes immediately to mind. to combine two vectors we do 1/(a-b)**2 on each dimension and then sum the results.

In the example above:

AB = 1 / (2-5.1)**2 + 1 / (5.1-5)**2 
   = 1/3.1**2 + 1/0.1**2 = 1/9 + 1/0.01 
  ~= 100

BC = 1 / (5.1-2.1)**2 + 1 / (5-1.1)**2
   = 1 / 3**2 + 1 / 3.9**2
   = 1 / 9 + 1 / 12
  ~= 1
  
AC = 1 / (2-2.1)**2 + 1 / (5.1-1.1)**2
   = 1 / 0.1**2 + 1 / 4**2
   = 1 / 0.01 + 1 / 16
  ~= 100

We see the desired result, where AB and AC are way bigger than BC giving us our “graph”.

I am not always interested in all dimensions, but only if they have some overlap. Even a combination of similar ones could work. But do similar items just dominate completely? What would be a cutoff for a graph? What when a concept is defined by a combination of vectors? How to evaluate the idea? This is currently a first thought, I didn’t even do research. This idea is so simple that it has to be done before.